Processing

This page tries to describe in reasonable detail what processing is done, how it is done, and what are the assumptions. It should enable advanced users and developers to review correctness and understand the underlying code. Any and all feedback or discussion on this description or the underlying code is welcomed on the developers list flraw-devel@lists.sourceforge.net ( Overview and options )

Gamma

Before anything else, I want to elaborate on gamma on which I believe a lot of confusion is existing.

When an image is gamma encoded, a mathematical relation is applied such that the encoded values are not linear proportional to the intensity of the captured light. Rather the encoding is such that in the most simple case EncodedValue = pow(LinearValue,1/2.2). (the precise function is dependent on system and environment but let's skip for the moment that detail).

In fact there are two reasons for doing so. The first one is nowadays probably the most important. Let's assume LinearValue is ranging from 0 to 100%. Then we get following encoded values :

LinearEncoded
0%0%
25%54%
50%73%
75%88%
100%100%

What you see is that the first 50% of linear values do use 73% of the available encoded values (f.i. 186 steps of 256 in a 8 bit system). This way much more detail (smaller steps) is kept in the low luminance areas then in the high luminance areas. Like much of our senses, the eye is heavily non-linear and is by far not as sensible in the high luminance areas as it is in the low luminance areas. This way we have an encoding that makes optimum use of the available encoding steps while our eye does not see the 'deceit'.

A second reason for this encoding (and becoming less important) is coming from CRT and TV technology. It happens that a CRT is not responding linear neither. The output light is about proportional to pow(AppliedVoltage,2.2). So if our image is now encoded with a gamma of 2.2 the two transformations cancel out :
LightOfCRT = pow(EncodedImage,2.2) = pow(pow(LinearLight,1/2.2),2.2) = LinearLight !

Linear processing in 16 bit

Nearly all image processing algorithms are linear and are assuming that the underlying representations are linear. When an image would be gamma-encoded as above, the algorithm gives wrong results.

However, when linear encoding is done, more bits are needed to keep the same 'accuracy' (technically spoken : Signal to Noise Ratio, SNR). Suppose for instance that you have a gamma encoded 8 bit system. Then the encoded value 1/256 corresponds to pow(1/256,2.2) = 5.034e-6. So that's the first fine step representable. When linear encoded, all steps would be equal to 1/256 = 3906e-6, so it is about 1000 times less precise. To obtain the same precision, a number of encoded values of 1/5.034e-6 = 198668 is needed. This would need 18 bits. Let's see however in some more detail to the first encoding steps of a gamma encoded 8 bit system :

Encoded valueLinear ValueStep Needed ValuesNeeded bits
00
1/2565.034e-65.034e-6 19864918
2/25623.13e-618.10e-6 5524816
3/25656.43e-633.30e-6 3003015

One can learn from the table that except for the very first quantization step the same precision (SNR) is reached with 16 bits or less as in a gamma encoded 8 bit representation. It is generally accepted that operations in a 16 bit linear encoded representation give sufficient precision.

flRaw does all of its operations on a 16 bit linear representation !

Here follow some links that might clarify the points made above :

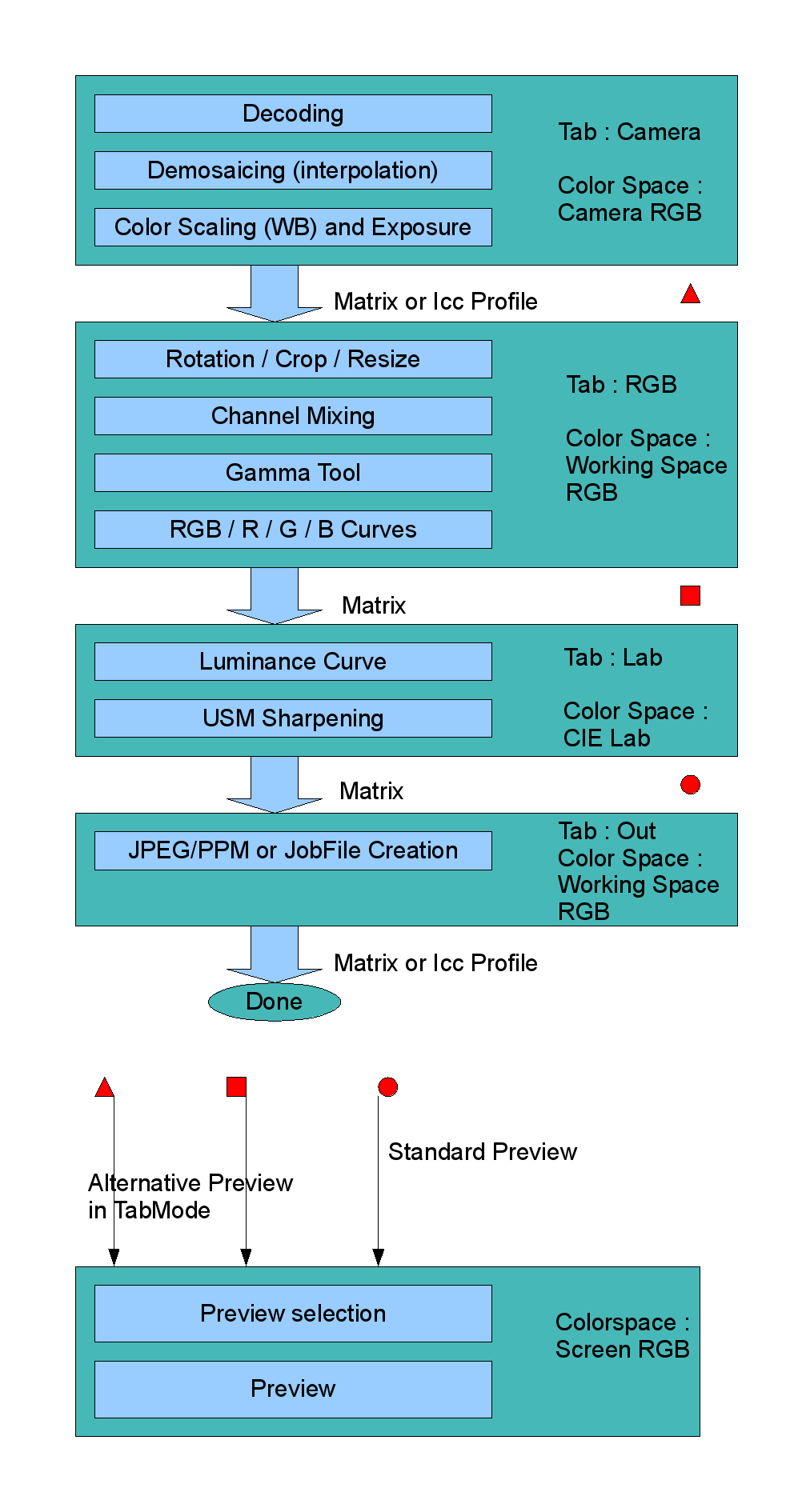
Simplified representation of the graphical pipe - workflow

Following image shows the different operations that can be done on an image. Also it is shown in which colorspace they are done and it is indicated to which 'tab' in the application it is linked.

Remark : the red shapes are as well reference points where a preview can be done as places where the image data are cached for performance.

Detailed description of the graphical pipe

Phase in 'RunPipe' (flGuiMain.cxx) Key function call Description Influential parameters
Phase=1, SubPhase=1 flDcRaw::Identify() Identify Image, Camera, Raw sizes and depending on the type of raw also some other settings.
All coming from dcraw.		 TheDcRaw->m_UserSetting_InputFileName
Phase=1, SubPhase=1 flDcRaw::RunDcRaw_Phase1() Decode Image, Remove bad pixels, Subtract darkframe.
All coming from dcraw.
When TheDcRaw->m_UserSetting_HalfSize = 1 then 2X2 pixels of the Bayer array are mapped onto one pixel of the Image. This way no interpolation is needed anymore and an important speedgain is made. This feature is coded into the BAYER(row,col) macro.
Further also m_MatrixSRGBToCamRGB is calculated here from m_MatrixCamRGBToSRGB. The latter in turn is a not yet (fully) understood function from TheDcRaw->m_UserSetting_CameraMatrix, TheDcRaw->m_UserSetting_CameraWb which sometimes throws in another matrix (m_cmatrix). 		TheDcRaw->m_UserSetting_HalfSize TheDcRaw->m_UserSetting_BadPixelsFileName TheDcRaw->m_UserSetting_DarkFrameFileName (TheDcRaw->m_UserSetting_CameraMatrix) (TheDcRaw->m_UserSetting_CameraWb)
Phase=1, SubPhase=2 flDcRaw::RunDcRaw_Phase2() flDcRaw::flCalcMultipliers() Calculate the multipliers to establish a correct whitebalance.
Largely taken from dcraw. Unlike dcraw however, the color scaling is not yet done at this phase.
The multipliers can be obtained from user input (TheDcRaw->m_UserSetting_Multiplier) or from a 'greybox' (TheDcRaw->m_UserSetting_GreyBox) that can ultimately extend to the whole image (TheDcRaw->m_UserSetting_AutoWB). Also the whitebalance can be taken from the camera (TheDcRaw->m_UserSetting_CameraWb). Whitebalance from camera can be obtained because the camera provides the multipliers or because the camera provides a sample grey area.
The result of this operation is TheDcRaw->m_Multipliers[]. 		TheDcRaw->m_UserSetting_Multiplier TheDcRaw->m_UserSetting_CameraWb TheDcRaw->m_UserSetting_AutoWb TheDcRaw->m_UserSetting_GreyBox TheDcRaw->m_UserSetting_BlackPoint TheDcRaw->m_UserSetting_Saturation
Phase=1, SubPhase=3 flDcRaw::RunDcRaw_Phase3() flDcRaw::flScaleBlack() flDcRaw::pre_interpolate() flDcRaw::lin_interpolate() flDcRaw::vng_interpolate() flDcRaw::ppg_interpolate() flDcRaw::ahd_interpolate() Interpolation (Demosaicing)
Largely taken from dcraw.
First the m_BlackLevel is subtracted from the image.
Then a 'preinterpolation' is done, but in fact this boils down to equalizing G1 to G2 or postpone that if TheDcRaw->m_MixGreen = 1 (which is the case if m_UserSetting_FourColorRGB=1 or m_UserSetting_HalfSize=1). m_Filters is adapted accordingly or set to 0 if m_UserSetting_HalfSize=1 (because then no interpolation is needed) Also dimensions are adapted in case of m_UserSettingHalfSize=1.
Then , if there is still a Bayer (m_Filters) , interpolation is done according to one of the 4 algorithms determined by TheDcRaw->m_UserSetting_Quality : linear,vng,ppg or ahd.
Finally, if needed, also 'green mixing' is done. 		TheDcRaw->m_UserSetting_HalfSize TheDcRaw->m_UserSetting_FourColorRGB TheDcRaw->m_UserSetting_Quality
Phase=1, SubPhase=4 flDcRaw::RunDcRaw_Phase4() flDcRaw::flDevelope() Exposure
Calculate a correction (exposure normalization) in case of EOS camera. This idea is coming from ufraw and it seems indeed needed to have a decent default exposure.
Then the normal exposure normalization is calculated on the basis of 1/MinimalPreMultiplier.
Also that exposure can be determined by the usersetting TheDcRaw->m_UserSetting_flRaw_ExposureCorrection.
Alternatively, when flDcRaw->m_UserSetting_flRaw_AutoExposure=1, an exposure is calculated that brings a fraction flDcRaw->m_UserSetting_flRaw_WhiteFraction (default 0.1) of the pixels above the 90% level.
Finally, the exposure correction is applied along with the colorscaling (Multipliers from Phase2).
For the clipping that might occur, two parameters are used : TheDcRaw->m_UserSetting_flRaw_ClipFactor determines how much of the value above the clipvalue is taken into account for the final value. 0 would result in no clipping at all, 1 would be full clipping. A default of 0.2 is used. TheDcRaw->m_UserSetting_flRaw_ClipLevel determines from what point on clipping is started. 0 would be from the maximum value before exposure correction. 1 would be from the maximum after exposure correction. (default) 		TheDcRaw->m_UserSetting_flRaw_EOSQuirk TheDcRaw->m_UserSetting_flRaw_AutoExposure TheDcRaw->m_UserSetting_flRaw_WhiteFraction TheDcRaw->m_UserSetting_flRaw_ClipFactor TheDcRaw->m_UserSetting_flRaw_ClipLevel
Phase=1, SubPhase=5 flImage::Set() Working space conversion.
The Image in TheDcRaw is in the color space of the camera, which is some variant on an RGB color space.
In previous phases also TheDcRaw->m_MatrixCamRGBToSRGB was obtained, be it via matrices delivered by the camera itself, be it by (Cam RGB -> XYZ) matrices delivered by Adobe (TheDcRaw::adobe_coeff).
This matrix (or a profile) will be used to convert to the working RGB color space.
  • When no Icc profile is defined :
    Following chain of matrices is used : TheDcRaw->m_MatrixCamRGBToSRGB => MatrixRGBToXYZ[flSpace_sRGB_D65] => MatrixXYZToRGB[TargetWorkingSpace].
  • When an Icc profile is defined :
    The profile is used in a cmsCreateMultiprofileTransform to transform into the TargetWorkingSpace.
    Note that also in this case no gamma is added in this transform, i.e. the result is in the target space but linear encoded !
    On the net there are hanging around a number of profiles that are clearly not profiled starting from the camera rgb space, but from some intermediate rgb space. Nobody knows for sure what this intermediate space is but I assume it is sRGB. Therefore one can opt here to apply an optional sRGB profile before the main profile. Nevertheless this stays a poor solution (other programs took other poor solutions). The only relevant profile would be one that is profiled from the camera space directly, such as could be done with lprof
GuiSettings->m_WorkColor GuiSettings->m_CameraProfileName GuiSettings->m_GammaBeforeCameraProfileName
Phase=2 flImage::Rotate()
flImage::Crop()
flImage::Resize()
flImage::MixChannels()
flImage::ApplyCurve(GTool)
flImage::ApplyCurve(RGB)
flImage::ApplyCurve(R)
flImage::ApplyCurve(G)
flImage::ApplyCurve(B)
  • Rotate
    A Rotation by 3 shears algorithm is used for rotation over an arbitrary angle.
  • Crop
    Part of the image can be cropped from the preview. Some support is in place for cropping in a predefined ratio H/W. Cropped sizes on the preview are calculated back to the relevant sizes on the full size image.
  • Resize
    A bilinear interpolation resizing algorithm is used.
  • Channel Mixer
    In the Channel Mixer the RGB channels are remixed. For each target R,G,B one can define how much of the original R,G,B is transferred to the target RGB. There are a few applications for that, the most known being to make a B/W picture. In that case each of the targets R,G,B is getting an equal amount of the original R,G,B. For instance Target R = Target G = Target B = 30%R + 59%G + 11%B. A number of interesting presets is defined.
  • Gamma Tool
    This is a weird ad-hoc part on which I really would like to receive thoughts and explanations. It is a curve transformation that adds some gamma like compression to the image, in such a way that , in an sRGB working space, the resultiong gamma after application of the sRGB gamma becomes as described best by the function itself :

    double GammaTool(double r, double Gamma, double Linearity) {
    const double g = Gamma * (1 - Linearity) / (1-Gamma*Linearity);
    const double a = 1/(1 + Linearity*(g-1));
    const double b = Linearity * (g-1)*a;
    const double c = pow((a*Linearity+b),g) / Linearity;
    return r<Linearity ? c*r : pow (a*r+b,g); }

    It is originating from the observation that when applying this gamma to the image it simply looks better than applying the standard sRGB which looks 'foggy'. This was at occasions discussed on the ufraw lists, but I don't believe it was ever explained adequately.
  • RGB,R,G,B Curves
    A curve is applied onto the image. With this all kind of tonal effects, like mimicking of filmcurves etc., can be obtained. An RGB curve is applied equally on all three the RGB channels. The R,G,B curves are applied on their respective channel only.
    There are internally two types of curves : 'Anchor' or 'Full'. The 'Anchor' curve is obtained by cubic spline interpolation on a number of anchors. The curve is editable by (re)moving or adding anchors. The 'Full' curve is obtained by applying a mathematical function that fully describes the curve. Those ones are not editeable. (The GammaTool curve as described above would be such one).
GuiSettings->m_Rotate GuiSettings->m_Crop GuiSettings->m_CropX GuiSettings->m_CropY GuiSettings->m_CropW GuiSettings->m_CropH GuiSettings->m_Resize GuiSettings->m_ResizeW GuiSettings->m_ResizeH GuiSettings->m_EnableChannelMixer GuiSettings->m_ChannelMixer GuiSettings->m_EnableGamma GuiSettings->m_Gamma GuiSettings->m_Linearity GuiSettings->m_HaveCurve[]
Phase=3
flImage::ApplyCurve(L)
flImage::USM()

Conversion to Lab colorspace, at least if one of the following operations is effectively requested.
  • Apply L Curve
    This curve transformation is applying a curve transformation but only on the L (=luminance) channel of Lab. This is thus a good way to implement luminance curves. For the remainder, the curves and curve editors are the same as the earlier RGB curves.
  • USM sharpening
    A pretty standard USM sharpening is applied.
    The parameters :
    • Radius: The radius of the Gaussian kernel in pixels.
    • Sigma: The standard deviation of the Gaussian. In pixels.
    • Amount: The percentage of the difference between the original and the blur image that is added back into the original.
    • Threshold: The threshold in pixels needed to apply the diffence amount.
GuiSettings->m_HaveCurve[flCurveChannel_L] GuiSettings->m_USM GuiSettings->m_USMRadius GuiSettings->m_USMSigma GuiSettings->m_USMAmount GuiSettings->m_USMThreshold
Phase=4
flImage::RGBToRGB() 		Conversion to output color space.
As well documentation as implementation need to be completed. 		GuiSettings->m_OutputColor

Encoding of values

Encoding of values is as suggested by ICC. This means - and to a certain extent this was validated - that matrix operations in flRaw and profile operations are mutual compatible.

CIE XYZ :
Value Encoding
0.0 0x0000
1.0 0x8000
1.0+(32767/32768) 0xFFFF

LAB L* encoding :
Value Encoding
0.0 0x0000
100 0xFF00
100+(25500/65280) 0xFFFF

LAB a*,b* encoding :
Value Encoding
-128 0x0000
0 0x8000
127 0xFF00
127+255/256 0xFFFF